L'histoire du Traitement du Signal et des Images

1. Aperçu historique de la théorie des grandes matrices aléatoires

Née dans les années cinquante du siècle dernier, la théorie des matrices aléatoires de grandes dimensions a été conçue à l'origine pour répondre à certaines questions de physique mathématique. Constituée depuis en branche propre des mathématiques, elle connaît aujourd'hui un développement foisonnant et trouve des applications dans de nombreux domaines scientifiques tels l'analyse des systèmes quantiques désordonnés, la théorie des nombres, l'économétrie ou les réseaux biologiques. Dans les années quatre-vingt-dix, elle a fait son entrée dans le domaine du signal et des communications. Plus récemment, elle a trouvé de nombreuses applications en théorie de l'apprentissage.

Dans les années 1950, en étudiant les niveaux d'énergie de noyaux atomiques lourds, Eugene Wigner eut l'idée de représenter l'opérateur hamiltonien (inconnu) qui décrit les états quantiques de ces noyaux par une grande matrice aléatoire ayant une forme simple et générique. Le modèle considéré par Wigner était celui d'une matrice réelle symétrique \(X = [x_{ij}]\), de taille \(N\times N\), où les variables aléatoires \(x_{ij}\) sont iid (indépendantes et identiquement distribuées) à la contrainte de symétrie près, centrées et de variance unité. Les niveaux d'énergie du noyau étudié correpondent au valeurs propres \(\{\lambda_1, \ldots, \lambda_N \}\) de la matrice \(N^{-1/2} X\). Alors que le comportement de ces valeurs propres dépend de la loi des \(x_{ij}\), Wigner a montré que dans le régime des grandes dimensions où \(N\to\infty\), le comportement spectral global de \(N^{-1/2} X\) était universel dans le sens où il ne dépend plus de cette loi, un peu à la manière de la loi des grands nombres en probabilié. Plus précisément, en notant

$$\begin{equation} \mu_N = \frac 1N \sum_{i=1}^N \delta_{\lambda_i} \end{equation}$$

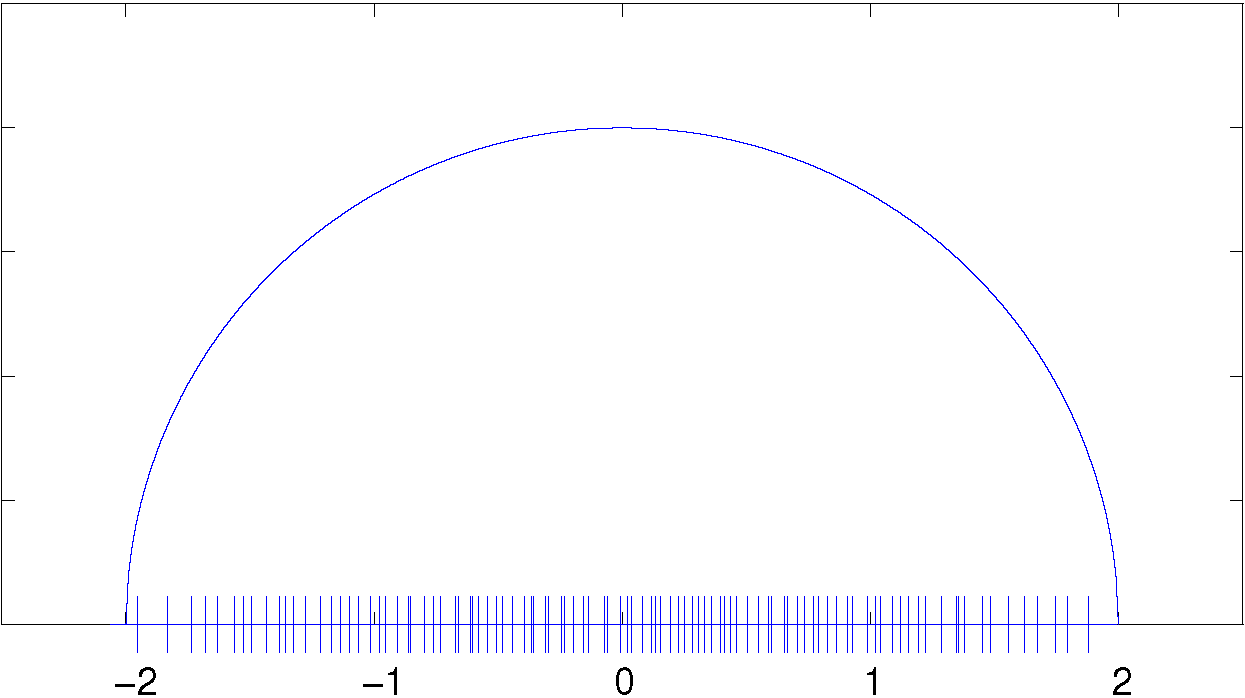
la mesure de probabilité aléatoire appelée la mesure spectrale de la matrice \(N^{-1/2}X\), Wigner a établi que \(\mu_N\) convergeait étroitement vers la mesure de probabilité déterministe dite la loi du demi cercle supportée par l'intervalle \([-2,2]\) (cf. figure 1.a).

Dix ans plus tard, Marchenko et Pastur étudièrent une deuxième classe de matrices aléatoires qui se trouve avoir plus d'applications que le modèle de Wigner dans les domaines des statistiques et du traitement du signal. Le modèle le plus simple considéré par ces auteurs est celui de la matrice de Gram \(\Sigma = n^{-1} XX^*\) où \(X \in \mathbb{C}^{N \times n}\) est une matrice aléatoire dont les éléments sont iid, centrés et de variance unité et \(X^*\) est la transposée conjuguée de \(X\). Supposons dans un premier temps que \(N\) soit fixe et que \(n\to\infty\). Dans cette situation, il est clair que la matrice \(\Sigma\) converge presque sûrement vers \(I_N\) par la loi des grands nombres, et par conséquent, que sa mesure spectrale \(\mu_N\) converge étroitement (au sens presque sûr) vers la mesure de Dirac \(\delta_1\).

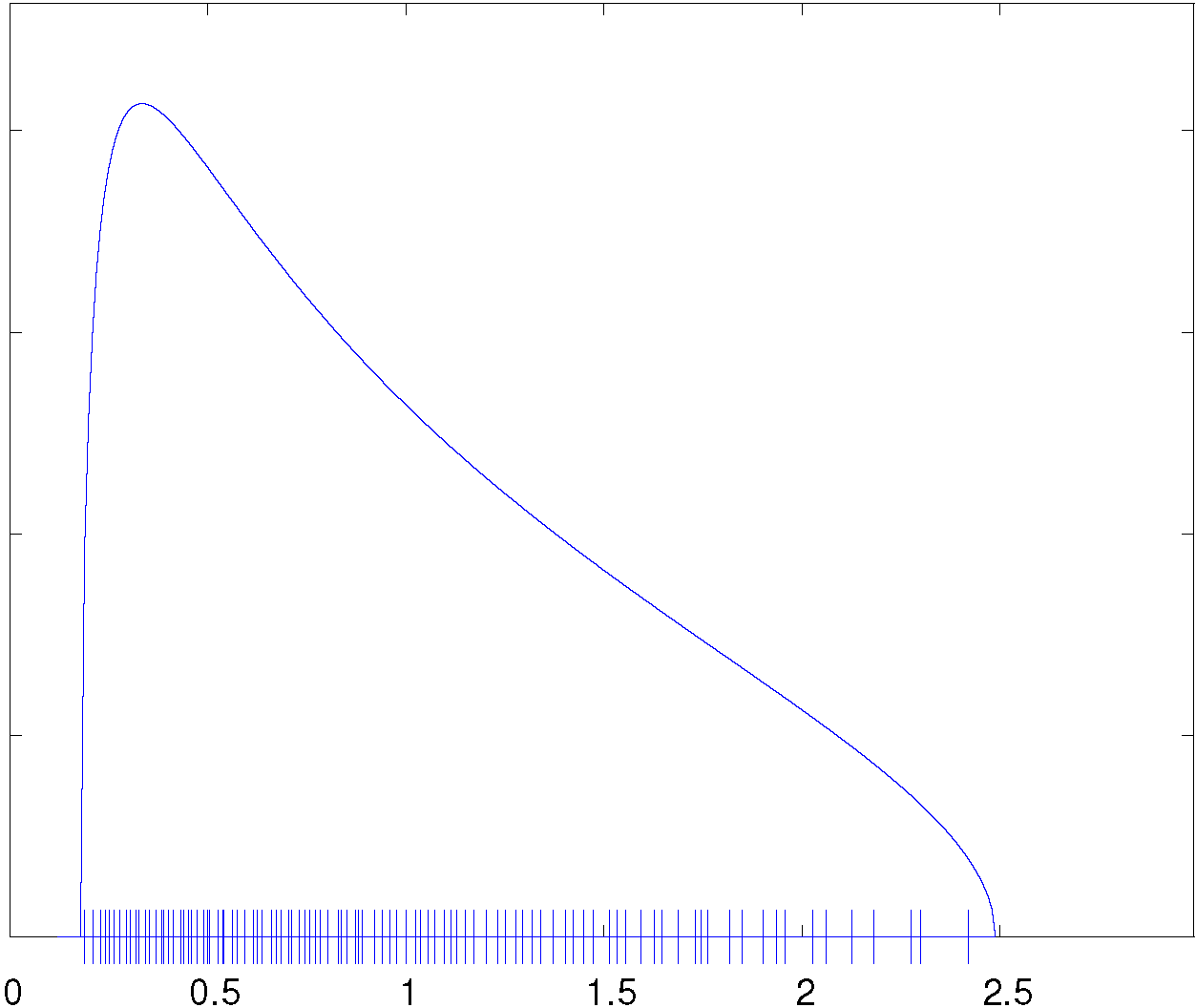
Marchenko et Pastur se sont intéressés à la situation plus complexe où \(N,n \to\infty\) de manière que \(N/n\) tende vers une constante \(c > 0\). Dans ce nouveau régime asymptotique, il demeure vrai que \(\Sigma\) converge vers \(I_N\) élément par élément par la loi des grands nombres, mais le comportement spectral de cette matrice change radicalement. Dans ce nouveau régime, la mesure spectrale \(\mu_N\) converge étroitement vers une nouvelle mesure de probabilité. Sur l'intervalle \(]0,\infty[\), cette mesure possède une densité supportée par l'intervalle \([(1-\sqrt{c})^2, (1+\sqrt{c})^2]\) (figure 1.b) et qui admet une expression explicite. Comme pour le cas de la matrice de Wigner, la convergence vers la loi de Marchenko-Pastur est universelle dans le sens où elle est vraie indépendamment de la loi des éléments de \(X\).

Depuis l'avènement des travaux de Wigner et de Marchenko et Pastur, un grand nombre de modèles de matrices aléatoires ont été étudiés. Ceux-ci comprennent des modèles à éléments corrélés, des modèles non centrés ou diverses associations de ceux-ci. La grande majorité de ces modèles ont en commun une propriété essentielle que nous énonçons d'une manière imprécise par le fait qu'ils possèdent \(\mathcal O(N^2)\) degrés de liberté : d'une façon ou d'une autre, la matrice \(N\times N\) considérée met en jeu \(\mathcal O(N^2)\) variables aléatoires indépendantes. Pour ces modèles, l'objectif premier est d'étudier la convergence étroite de la mesure spectrale \(\mu_N = N^{-1} \sum_{i=1}^N \delta_{\lambda_i}\) sans s'occuper des fluctuations individuelles des valeurs propres \(\lambda_i\). On parle du comportement macroscopique de la mesure spectrale.

En allant plus loin, Wigner s'est intéressé également au comportement microscopique des valeurs propres d'une grande matrice aléatoire. En raison de l'intérêt que présente l'étude fine des séparations entre les états du système quantique sous-jacent, la détermination de la loi des espacements entre les valeurs propres est en effet une question majeure.

Dans les années soixante, Gaudin, Mehta et Dyson montrèrent que dans l'intervalle \(]-2, 2[\), i.e., à l'intérieur du support de la loi du demi cercle, l'espacement typique entre les valeurs propres d'une matrice de Wigner gaussienne était de l'ordre de \(1/N\) et qu'à cette échelle, la loi asymptotique des fluctuations était décrite par la loi dite du sinus. Toujours dans le cas gaussien, les fluctuations asymptotiques de la plus grande valeur propre, identifiées au début des années \(90\), suivent un autre régime : l'espacement typique est de l'ordre de \(N^{-2/3}\) et la loi asymptotique est la loi dite de Tracy-Widom. Des résultats analogues existent pour le modèle \(n^{-1}XX^*\) gaussien. Ces résultats étant établis, il est naturel de lever l'hypothèse gaussienne sur les éléments de la matrice étudiée. Selon ce qui fut longtemps appelé la conjecture Wigner-Dyson-Mehta, le comportement microscopique des valeurs propres est universel (tout comme le comportement macroscopique), et ne dépend que du type du modèle probabiliste de la matrice étudiée (Wigner, Marchenko-Pastur, modèles corrélés, etc.). Dans la deuxième moitié des années 2000, cette conjecture a été vérifiée par Erdös, Schlein, Yau, et Yin. Des travaux parallèles ont été réalisés par Tao et Vu.

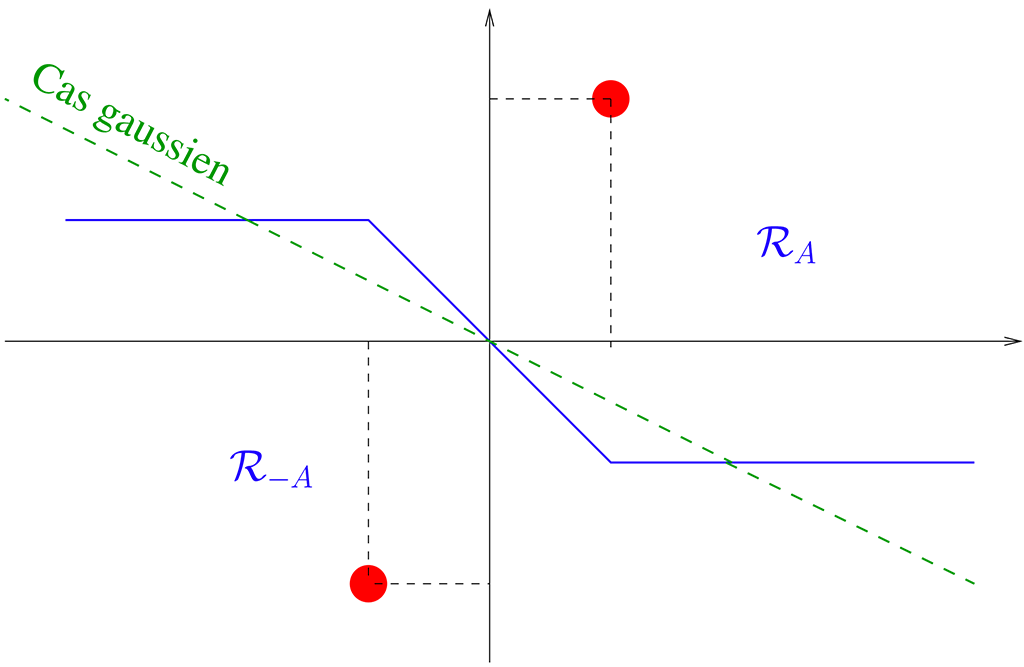
Une autre branche de la théorie, très utile pour les applications, concerne les perturbations de rang fini d'une grande matrice aléatoire. Revenons au modèle \(\Sigma = n^{-1} XX^*\) et supposons cette fois que \(X \in \mathbb{C}^{N\times n}\) soit de la forme \(X = A + W\) où \(W\) est une matrice à éléments iid, centrés et de variance unité et où \(A\) est une matrice déterministe de rang \(1\). En raison de son rang, la présence de la matrice \(A\) n'affecte pas le comportement macroscopique des valeurs propres de \(\Sigma\). La mesure spectrale de cette matrice converge toujours vers la loi de Marchenko-Pastur. Cependant, il peut arriver qu'une valeur propre isolée apparaisse en dehors du support de la loi de Marchenko-Pastur : dans le régime asymptotique \(N,n\to\infty\), si \(n^{-1/2} \| A \|\) dépasse un certain seuil, la plus grande valeur propre de \(\Sigma\) se détache du support de cette loi et converge vers une valeur déterministe que l'on peut déterminer (fig.~\ref{fig:outliers}). Dans le cas contraire, la plus grande valeur propre de \(\Sigma\) converge vers le bord droit du support de la loi de Marchenko-Pastur.

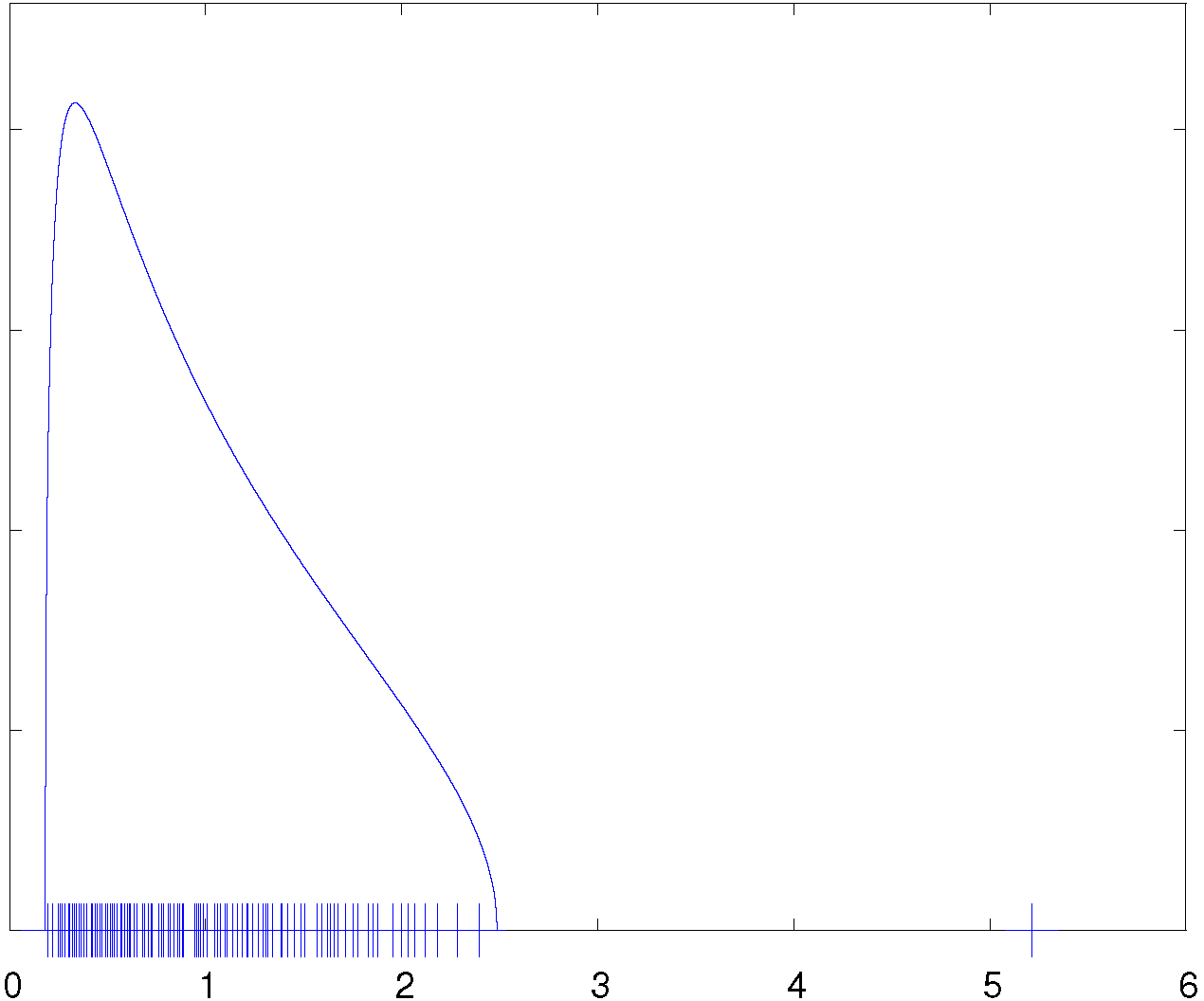
Cette <<transition de phase>> de la plus grande valeur propre a été mise en évidence dans le cas gaussien par Baik, Ben Arous et Péché en 2005. La théorie a été généralisée et adaptée à un grand nombre de modèles aléatoires. Des résultats sur les sous-espaces invariants associés aux valeurs propres isolées sont également disponibles.

Toutes les matrices aléatoires évoquées jusqu'ici dans cette note sont des matrices hermitiennes ou symétriques. Une branche de la théorie des matrices aléatoires s'attache à l'étude spectrale des matrices non hermitiennes (ou non symétriques). L'étude spectrale de ces dernières est plus tardive que celles de leurs homologues hermitiennes. Une difficulté importante liée à l'étude des matrices non hermitiennes provient du fait qu'en général, les valeurs propres d'une matrice carrée sont moins stables que ses valeurs singulières : une perturbation, aussi petite soit-elle, peut modifier drastiquement les premières alors que les secondes ne seront perturbées que d'une manière limitée. Grossièrement, la théorie des matrices aléatoires non hermitiennes montre que la sensibilité de la mesure spectrale aux perturbations est largement amoindrie quand la matrice en question est aléatoire et possède \(\mathcal O(N^2)\) degrés de liberté.

Le modèle de référence d'une matrice aléatoire non hermitienne est celui de la matrice \(N^{-1/2} X\) où \(X = [x_{ij}]\) est une matrice réelle ou complexe de taille \(N\times N\), à éléments iid, centrés et de variance unité. Comme les valeurs propres de \(N^{-1/2} X\) sont complexes, la mesure spectrale de cette matrice est supportée par \(\mathbb{C}\). La théorie des matrices aléatoires non hermitiennes montre qu'indépendamment de la loi des \(x_{ij}\), cette mesure converge presque sûrement vers la loi uniforme sur le disque unité. La preuve de ce résultat a une longue histoire. Dans les années 1960, Ginibre l'établit pour le cas gaussien complexe. Vingt ans plus tard, Girko proposa une approche pour traiter le cas général, basée sur l'utilisation du potentiel logarithmique et l'idée d'<<hermitisation>>. Les idées de Girko ont inspiré une série de travaux qui culminèrent avec les travaux de Tao et Vu publiés en 2010.

Les modèles statistiques plus sophistiqués que le modèle iid, les lois locales et les perturbations de rang fixe ont également été étudiés dans le cas non hermitien.

2. Applications dans le périmètre scientifique du traitement du signal

Depuis le milieu des années 90, les applications de la théorie des matrices aléatoires en communications numériques, en traitement du signal, en estimation statistique et en théorie de l'apprentissage sont innombrables. L'exposé ci-dessous n'a aucune prétention à l'exhaustivité.

2.1 Communications sans fil

L'une des premières applications de la théorie des grandes matrices aléatoires dans ces domaines avait pour objet les communications numériques sans fil. En raison de la mobilité et de la présence d'une multitude de réflecteurs et de diffuseurs sur le chemin des ondes radio, la matrice \(X \in \mathbb{C}^{N\times n}\) qui représente un canal MIMO (<< Multiple Input Multiple Output >>) reliant \(n\) émetteurs à \(N\) récepteurs est le plus souvent décrite par un modèle aléatoire. Dans ce cadre, l'analyse de la mesure spectrale de \(\Sigma = n^{-1} XX^*\) permet d'évaluer l'information mutuelle de Shannon de ce canal dans le régime où les nombres d'antennes \(n\) et \(N\) sont grands et comparables. Cette analyse donne une assise théorique au fait bien connu que la capacité de Shannon d'un canal MIMO << croît linéairement en le nombre d'antennes >> pour peu que le canal renferme \(\mathcal O(N^2)\) degrés de liberté. Une intense activité de recherche dans ce domaine, inaugurée par le travail de Telatar (1995), a porté sur les systèmes MIMO et << MIMO massifs >>, les systèmes à accès multiple utilisés dans les systèmes 3G, 4G et 5G et d'autres. La plupart de ces résultats sont basés sur le comportement macroscopique des spectres de modèles de plus en plus sophistiqués de matrices aléatoires.

Les résultats microscopiques, notamment ceux relatifs aux fluctuations des valeurs propres près du bord de la mesure spectrale ainsi que les résultats sur les perturbations de rang fixe ont également servi à étudier des algorithmes de détection de signaux radio ou d'inférence statistique pour les communications sans fil.

2.2 Estimation statistique multivariée

L'intérêt de la théorie des grandes matrices aléatoires en statistiques prend sa racine dans le fait que les dimensions des données observées dans la plupart des applications récentes sont très grandes. Citons en guise d'exemples le grand nombre d'attributs en apprentissage statistique, de n\oe uds dans les applications d'inférence sur les réseaux, de capteurs dans les réseaux d'acquisition distribuée ou d'antennes en radio astronomie.

L'utilité de la théorie des grandes matrices aléatoires dans ce domaine provient du fait qu'il n'est pas toujours possible de supposer que la taille \(n\) de la fenêtre d'observation d'une série statistique observée soit beaucoup plus grande que la dimension \(N\) de cette série. Cela peut être dû au fait qu'une durée d'observation compatible avec l'hypothèse de stationnarité est souvent limitée. Dans ces conditions, l'hypothèse classique selon laquelle \(N\) est fixe et \(n \to\infty\) perd de sa pertinence. Il est souvent plus réaliste de la remplacer par l'hypothèse où \(N,n \to\infty\) à la même vitesse.

A titre d'exemple, supposons que cette série multivariée soit représentée par une matrice \(Y \in \mathbb{C}^{N\times n}\) de la forme \(Y = R^{1/2} X\) où \(X \in \mathbb{C}^{N\times n}\) une matrice à éléments iid centrés de variance unité et \(R\) une matrice de covariance déterministe et inconnue. En traitement d'antennes, en économétrie ou dans d'autres domaines d'application, l'enjeu est souvent de mettre en place un algorithme d'inférence statistique sur les valeurs propres ou sur certains espaces propres de \(R\). Les algorithmes d'inférence classiques, conçus pour le régime asymptotique où \(N\) est fixe et \(n\to\infty\), perdent leur consistance dans le régime asymptotique qui nous intéresse. Un des succès de la théorie des matrices aléatoires a été de proposer des algorithmes d'estimation consistants dans ce nouveau régime asymptotique.

La théorie ne s'est pas restreinte aux modèles simples du type \(Y = R^{1/2} X\). Récemment, des modèles plus sophistiqués tels les modèles de traitement d'antennes à bande large ou les modèles à spectre rationnel décrits par des équations d'état ont été considérés.

D'autres directions de recherche ont été explorées : parmi celles-ci, l'inférence pour des modèles de perturbation de rang fini du type \(W+A\) (cf ci-dessus) où l'information pertinente est portée par la matrice de rang faible \(A\) et où \(W\) est une matrice de << bruit >>, ou les algorithmes d'estimation robuste, tels les << M-estimateurs >>, qui résistent à des bruits de nature impulsive.

2.3 Apprentissage et intelligence artificielle

La théorie des matrices aléatoires de grandes dimensions se trouve au c\oe ur d'un grand nombre de problèmes d'apprentissage et d'intelligence artificielle. Citons :

• La détection de communautés sur les graphes. Dans ces problèmes, il est naturel de modéliser la matrice d'adjacence, la matrice laplacienne ou d'autres par une matrice aléatoire symétrique ou non selon la nature du graphe sous-jacent. En général, l'information sur les communautés est structurellement incluse dans une composante de rang fini noyée dans du bruit. La théorie des matrices aléatoires, parfois couplée avec des outils issus de la physique statistique rend possible l'extraction de cette information.
• L'inférence statistique sur des matrices à noyaux. Dans les problèmes de classification des données structurées, l'objet de base qui sert à réaliser la classification est une matrice aléatoire dite << à noyau >>, dont l'élément \((i,j)\) est obtenu par l'application d'un opérateur d'affinité entre les vecteurs de l'attribut \(i\) et celui de l'attribut \(j\). L'analyse spectrale d'une telle matrice permet de développer des classifieurs efficaces dans le régime asymptotique où le nombre de vecteurs et leur dimension sont grands et comparables.
• L'analyse de performance des réseaux de neurones artificiels. La sortie d'une couche dans un réseau de neurones peut être représentée par une matrice aléatoire de la forme \(\sigma(X)\) où \(\sigma(\cdot)\) est la fonction non linéaire d'activation appliquée élément par élément à une certaine matrice aléatoire \(X\). Cette dernière est une matrice structurée construite à partir des données d'apprentissage et des poids du réseau. L'analyse spectrale de \(\sigma(X)\), et plus généralement, des compositions de ces objets au travers des couches du réseau, met la lumière sur les performances du réseau de neurones.

Cette liste n'épuise pas les utilisations de des grandes matrices aléatoires en théorie de l'apprentissage. Les liens de cette théorie avec la théorie des probabilités en grande dimension, la physique statistique ou la théorie de l'optimisation sont activement explorés dans la recherche contemporaine.

Pour aller plus loin

[Abb17] E. Abbe. Community detection and stochastic block models : recent developments. J. Mach. Learn. Res., 18 :Paper No. 177, 86, 2017.
[CD11] R. Couillet and M. Debbah. Random matrix methods for wireless communications. Cambridge University Press, Cambridge, 2011.
[ts16] (num ero sp ecial sur les matrices al eatoires). Traitement du Signal, 33(2-3), 2016.
[Ver18] R. Vershynin. High-dimensional probability, volume 47 of Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge, 2018. An introduction with applications in data science.
[Wai19] M. J. Wainwright. High-dimensional statistics, volume 48 of Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge, 2019.